El largo camino hacia la predicción probabilista (VI). El caos entra en escena

En el camino hacia la predicción probabilista el caos entra en escena.

A lo largo de esta sexta entrega Mario Fernández nos habla acerca de la aportación de personajes tan ilustres como Urban Leverrier, Poincaré o Ian Stewart para seguir avanzando en el conocimiento de la predicción meteorológica.

Nuevo enfoque de las ciencias empíricas

Durante todo el siglo XIX la famosa cita de Laplace que citamos al final de este artículo, se convirtió en el paradigma del mecanicismo y del determinismo tanto a nivel de las ciencias empíricas como a nivel del pensamiento filosófico.

Dicho paradigma estaba muy extendido debido a los espectaculares triunfos de la mecánica newtoniana.

Recordemos que fue gracias a esta que Leverrier pudo descubrir el planeta Neptuno por las irregularidades en la órbita de Urano, unas irregularidades que, suponía con acierto Leverrier, eran debidas a las interacciones gravitatorias del propio Urano con un planeta no descubierto aún.

Urban Leverrier convenció al astrónomo Johann Gotfried Gaalle para que iniciara la búsqueda del nuevo cuerpo celeste y así este apareció en el firmamento el 23 de septiembre de 1846 en el lugar predicho según los cálculos del mismo Leverrier. 

Conocer las condiciones iniciales

A mediados del siglo XIX, como se ve, el problema de dar con una hipótesis universal que lo explicase todo a nivel macroscópico y microscópico se reducía a una simple cuestión de conocer las llamadas “condiciones iniciales”.

Corría el año 1887 y el rey Óscar II de Suecia y Noruega, monarca aficionado a las Matemáticas, ofreció un premio de 2500 coronas por una respuesta a una cuestión fundamental en Astronomía: ¿es estable el Sistema Solar?

Aquí debemos entender por “estable” si, con el transcurso del tiempo, el sistema permanece invariable, si no cambia debido a pequeñas perturbaciones.

¿Continuarán los planetas moviéndose aproximadamente por sus órbitas habituales?

¿Podría la Tierra derivar al espacio frío y oscuro?

Cuando tenemos dos cuerpos únicamente de los que conocemos sus posiciones y velocidades y sometidos ambos a una atracción gravitatoria mutua, independientemente de la cuantía de sus masas, las ecuaciones de la mecánica newtoniana predicen en cualquier momento su evolución futura.

Si a estos dos cuerpos en interacción mutua añadimos uno más, el problema se complica enormemente y no digamos ya si consideramos todos los planetas, satélites, cometas y otros pequeños cuerpos que lo componen, todos en interacción gravitatoria mutua.

El Problema de los Tres Cuerpos y las ecuaciones de la dinámica

El matemático Poincaré publicó una memoria por la que le fue concedido el premio del rey Óscar y que tituló (en francés) El Problema de los Tres Cuerpos y las ecuaciones de la dinámica.

Dicha memoria fue publicada en el año 1890 y constaba de unas 270 páginas con dos partes diferenciadas: en la primera se describían y se establecían las propiedades de las ecuaciones dinámicas y en la segunda se aplicaban los resultados de dichas ecuaciones aplicadas a un número arbitrario de cuerpos (al como el Sistema Solar) moviéndose y sometidos a la atracción gravitatoria newtoniana.

El sistema Sol-Tierra

Con sólo dos cuerpos, el conjunto de soluciones que proporcionaban dichas ecuaciones, era periódico; es decir, se repiten una y otra vez por siempre (por ejemplo, en el sistema Sol–Tierra y el tiempo necesario para que se dé esta repetición, esta periodicidad, es de un año.

En este periodo de un año, sabemos que la Tierra ni se precipita contra el Sol ni se alejará más allá del infinito).

El hecho de que un sistema sea periódico, informa de forma muy directa sobre su estabilidad.

Poincaré luchó mucho para demostrar que existían soluciones periódicas cuando eran más de dos los cuerpos involucrados y demuestra cómo obtener dichas soluciones desarrollando la variable involucrada mediante una serie infinita en donde cada término es función periódica de la variable tiempo.

“De ello resulta -dice- que existen series cuyos coeficientes son periódicos y que satisfacen formalmente las ecuaciones”.

También dice que “queda por demostrar la convergencia de esta serie”. Él lo creía pero no lo demostró y declina embarcarse en dicho cálculo.

La sección de Poincaré

Básicamente el tratamiento que dio Poincaré al problema de los tres cuerpos es un tratamiento basado en propiedades topológicas.

Así nació la llamada sección de Poincaré en un intento de encontrar soluciones periódicas que pudieran determinar la estabilidad de un sistema, pero tomando sólo en cuenta algunos estados iniciales.

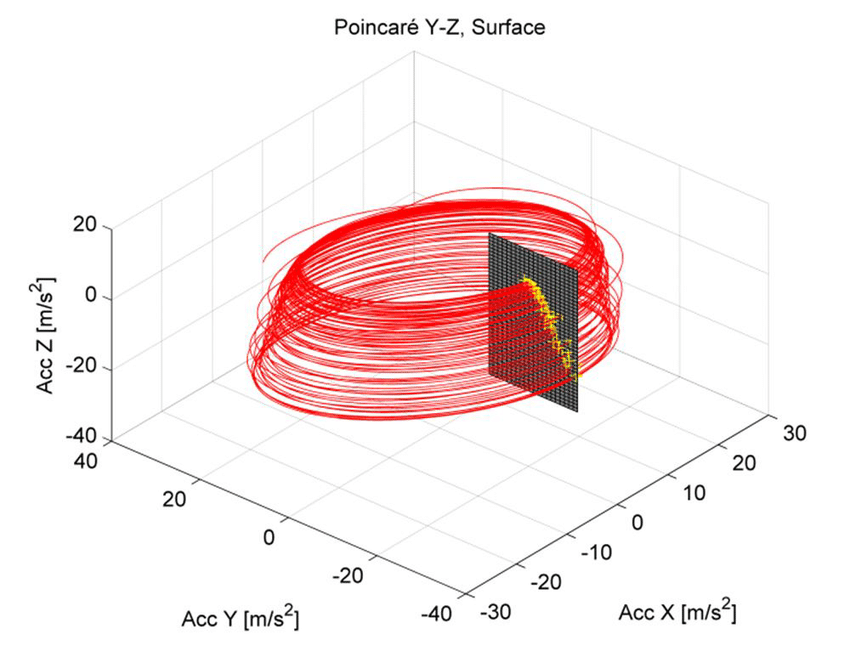
Poincaré decidió emplear sus recién descubiertos métodos al denominado método reducido de Hill que no es más que una simplificación del problema de los tres cuerpos donde uno de estos cuerpos que forman el sistema original de tres tiene una masa tan reducida que no afectaría a la marcha de los otros dos, pero de forma paradójica, los dos cuerpos de masa mayor sí afectan a la marcha del cuerpo con masa despreciable.

¿Juega Dios a los dados?

Ian Stewart, en su libro ¿Juega Dios a los dados? supone un sistema formado por los planetas Neptuno, Plutón y una mota de polvo interestelar.

Tanto Plutón como Neptuno se moverán en una elipse, pero no así la mota de polvo interestelar que mostrará una trayectoria oscilante y dependiente de las atracciones gravitatorias que sobre ella ejercen tanto Neptuno como Plutón.

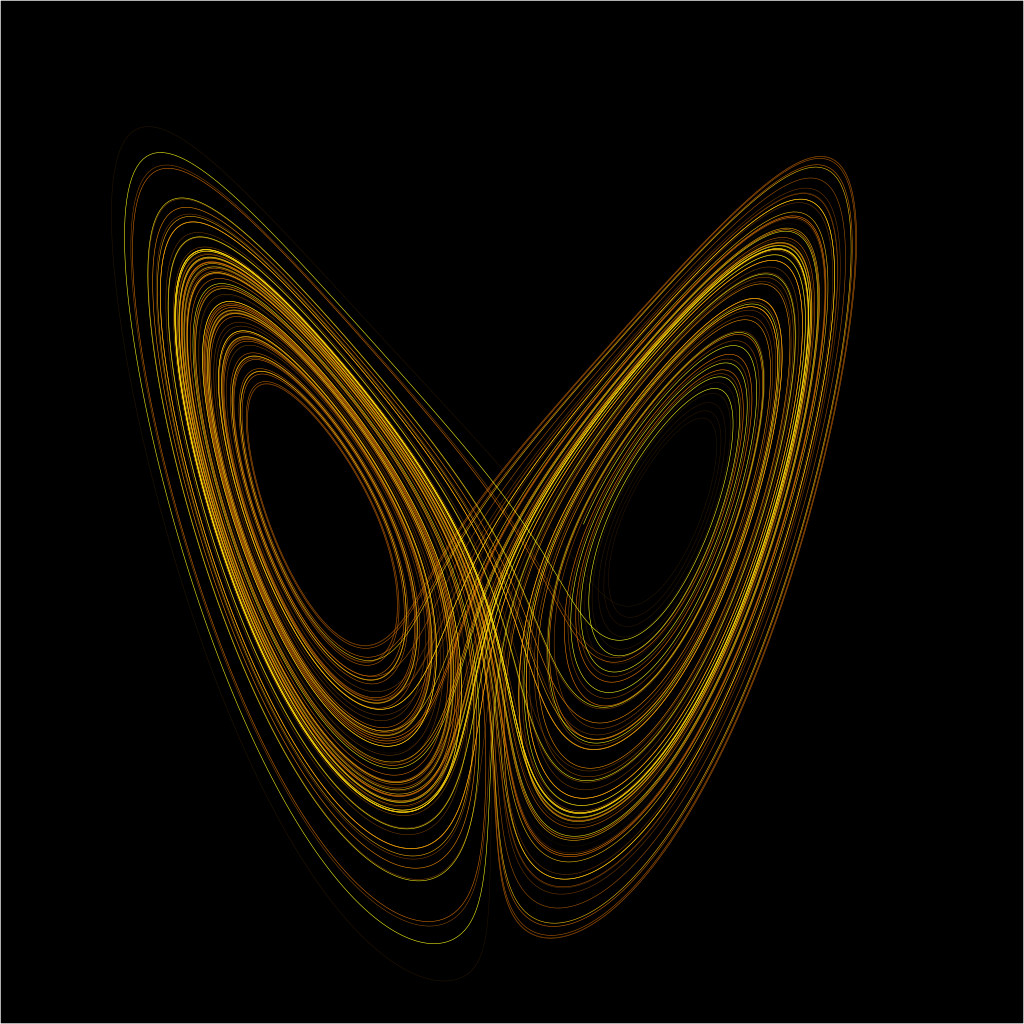
Poincaré llega a la conclusión de que el comportamiento gravitatorio de la mota de polvo es tan complicado que escribe en el tercer volumen de su obra, Nuevos Métodos de Mecánica Celeste:

“Cuando uno intenta dibujar las figuras formadas por estas dos curvas y su infinidad de intersecciones…estas intersecciones forman una especie de red, de tela de araña o malla infinitamente enredada…

Uno topa con la complejidad de esta figura que ni siquiera me atrevo a dibujar. Nada puede darnos una idea mejor sobre la complejidad del problema de los tres cuerpos”.

El abuelo del caos

Ya para concluir diremos que el tratamiento que dio Poincaré al problema de los tres cuerpos lo puso directamente en contacto con un nuevo paradigma matemático y del que nació la llamada Teoría del Caos que, pasada la primera mitad del siglo XX, desarrollaría Edward Norton Lorenz en toda su plenitud.

Con toda justicia puede llamarse a Poincaré el abuelo del Caos, el primero que, partiendo de ecuaciones deterministas, se dio completamente de bruces con él.

Luego ya llegaría el nacimiento de la Mecánica Cuántica para poner fin al paradigma determinista en la Física y que tan bien condensaba la proposición de Laplace con la que hemos abierto este capítulo.

Bibliografía

• Stewart, Ian. ¿Juega Dios a los dados? Edit Crítica. Dakontos de bolsillo.4ª Edic año 2010.Barcelona.
• Ilustraciones:
• -Wikipedia.
• -Slideshire. El problema de los tres cuerpos.
• “¡Dejad que brame el caos!
• ¡Dejad que las figuras de las nubes pululen!
• Yo espero que llegue la forma” (Robert Frost,poeta norteamericano).

Una inteligencia que en un instante dado supiera todas las fuerzas que actúan en la naturaleza y la posición de cada objeto en el universo – si estuviese dotada de un cerebro suficientemente vasto para hacer todos los cálculos necesarios – podría describir con una sola fórmula los movimientos de los mayores cuerpos astronómicos y los de los átomos más pequeños. Para tal inteligencia, nada sería incierto, el futuro, como el pasado, serían un libro abierto.

Pierre-Simon Laplace